简单体积渲染

通常认为光线在空气中沿直线传播，并且不会衰减，但实际上，光线会与传输介质粒子发生一系列作用，可以理解为光线目前呈粒子性，与空气分子发生碰撞并偏离方向，损失一部分能量。

依据光子与粒子发生作用前后方向的改变和能量的变化，将这种作用分为四类：

1. 吸收，光子作用前后方向不变，但能量衰减

2. 发射，粒子本身可以向外界辐射，使光子传输方向上的能量增强，通常会忽略掉

3. 散射，光子与粒子发生作用后方向改变，向四周散射

4. 内散射，其余方向上的光子与粒子发生作用，使其朝当前方向散射

其中吸收作用即是光线传输中的透射现象，散射与内散射是散射现象，关注从空气粒子射向摄像机的方向，该方向上一个微小距离上的的能量变换应当如下公式：

$L{o}-L{i} = -吸收+发射-散射+内散射$

透射

光线在仅发生透射的时候，在各向同性的均匀介质中遵循比尔-朗博定律，

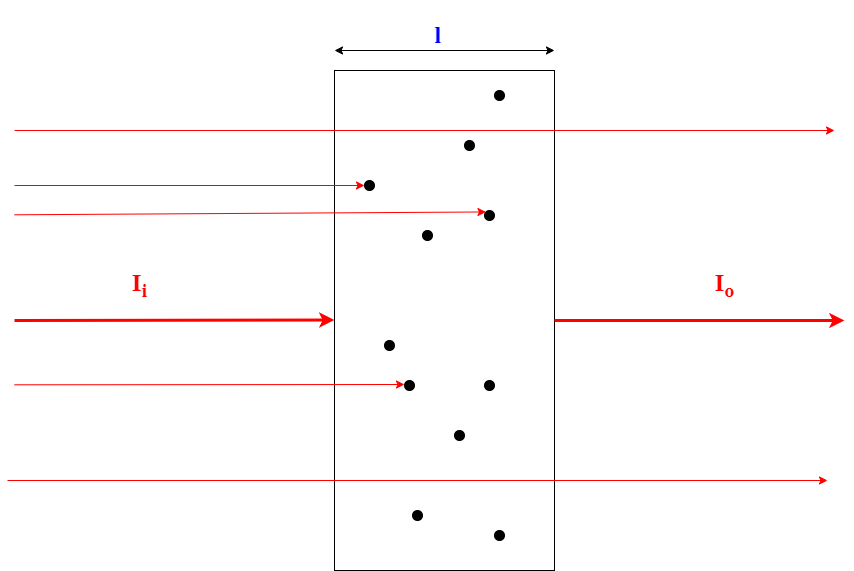
即$-log_{10}\frac{I_o}{I_i}=K\ast l\ast c=A=log_{10}\frac{1}{T}$

中$I_o$为透射光，$I_i$为入射光，$K$为吸收系数或摩尔吸收系数，$l$为介质厚度，$c$为介质浓度，$K$的单位应与其对应，$A$为吸光度，$T$为透光度

由于$K$和$c$需要针对具体场景进行设置，使用该公式并不方便，对其进行一些变动，定义$T=e^{-\tau}=10^{-A}$，则上述公式变为$\frac{I_o}{I_i}=e^{-\tau}，I_o=I_i\ast e^{\tau}$

其中$\tau=-ln{T}=A\ast ln{10}=K\ast l\ast c\ast ln10$称为光深，但是使用$\tau$直接描述了整个光路的透射性质，无法对内部某一点进行调整，

那么定义$\tau=\sigma\ast l$即$\sigma=K\ast c$，$\sigma$称为衰减系数，现在可以对具体一点的透射性质进行调整，调整后介质不再是均匀介质，那么现在的透射公式为$I_o=I_i\ast exp({\int^{l}_{0}{\sigma}dl})$

散射

散射不像透射统一遵循一个规律，根据作用粒子与光波长的比值，会分成数种情况讨论，且具体推导涉及到电磁场的内容，在此不进行推导，单就图形学而言，一般常用的只有Rayleigh（瑞利）散射和Mie（米氏）散射

将光线的入射方向作为坐标轴的x方向，光线散射后将偏离当前方向，由于对称性的存在，偏离的方向只需要一个坐标轴就可以表示，那么就形成了一个xy二维坐标轴，其中的方向向量表示散射后的方向，由于散射后会损失能量，假设入射光线能量为单位1，那么以所有方向上的散射光线可以画成一张图：

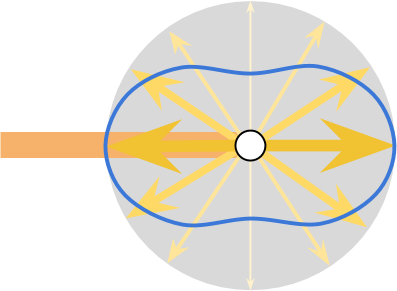
这张图称为散射相位图或相位函数

Rayleigh散射

通常认为当粒子大小是光波长的$\frac{1}{10}$的时候，发生Rayleigh散射，其相位函数呈哑铃状，即$\rho(\theta)=(1+cos^{2}{\theta})$

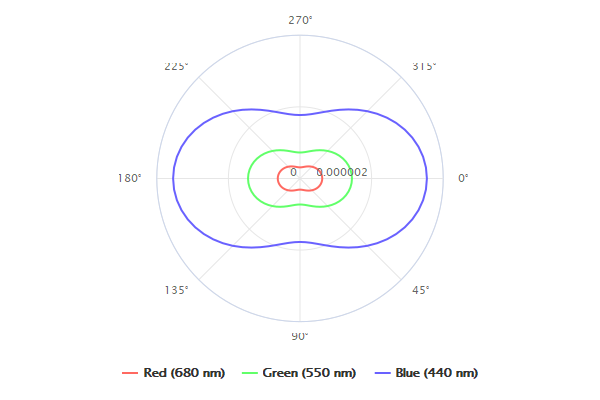
当考虑光的波长时，$\rho(\theta)\propto \frac{1}{\lambda ^{4}}$，空气中该Rayleigh散射是$I_o=I_i\ast \frac{\pi^2(n^2-1)}{2} \frac{\rho(h)}{N}\frac{1}{\lambda^4}(1+cos^2\theta)$，其中$n$是空气的折射率，$h$是海拔高度，$N$是标准大气分子数密度，$\rho(h)$是密度比，在海平面处为1，空气中的Rayleigh散射有许多公式，这是其中一个

Mie散射

当粒子大小与光线波长大致相同时，发生Mie散射，Mie散射带有很强的方向性。

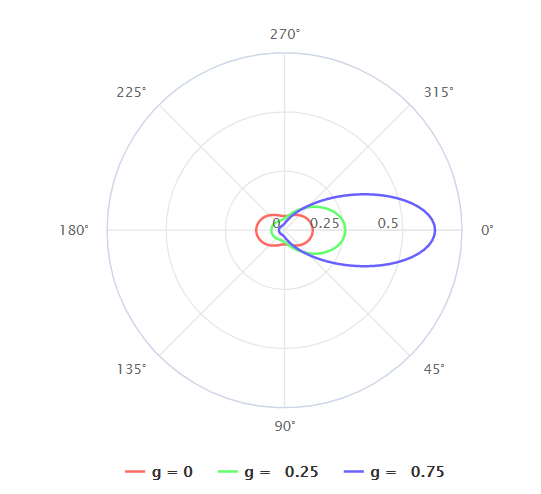
计算上比较复杂，一般而言会使用Henyey-Greenstein（HG）相位函数，表达式为$\rho(\theta,g)=\frac{1-g^2}{4\pi(1+g^2-2gcos\theta)^{1.5}}$，其中$g$参数用于控制方向，取值范围是$[-1,1]$

在大气渲染中这两个散射都有一些优化的计算方式以及预计算参数，这部分后续教程说明。

综合

以上给出了透射和散射的公式，但散射部分会引入别的方向上的光线进行计算，从而导致递归计算，导致计算量指数爆炸，简化情况下仅考虑散射导致的能量损失，此时散射的相位函数只需要$(1,0)$即x轴正方向上的值，此时该值与透射公式中的透光度类似，仿照$\tau$的定义，定义其为$T_s=e^{-\tau_s}$，那么光线透过介质的公式即为：

$I_o=I_i\ast exp(\int^{l}_{0}{(\tau_t+\tau_s)}dl)$

即为体积渲染的公式