环境光遮蔽

环境光照模型

在bling-phong模型和brdf的cook-torrance模型中，都假设了环境光照为一个常数，即 $L_{ambient}=k_{d}f_{lambert}$ ，以下给出该模型的理论依据

考虑一个仅由环境光照亮的场景，各着色点之间所受的辐射率应当相同，对其作出以下三个假设：

任意着色点所接收到的环境光相同
环境光的辐射率是各向同性的
着色点对于环境光仅产生各向同性漫反射，即lobe呈半圆状

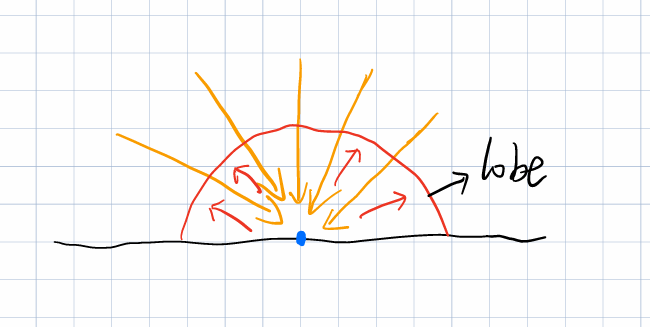
从渲染方程开始：

$L_{o}(p,\omega_o)=L_e(p,\omega_o)+\int_{\Omega^+}L_i(p,\omega_i)f_{brdf}(p,\omega_i,\omega_o)(\boldsymbol{n}\ast\boldsymbol{\omega_i})V(p,\omega_i)\mathrm{d}\omega_i$

上式中 $\Omega+$ 表示积分范围为法线方向半圆， $V(p,\omega_i)$ 表示可见性函数，在直接光照的场景中，由阴影提供

忽略自发光项，利用近似公式：

$\int_{\Omega}f(x)g(x)\approx\frac{\int_{\Omega_S}f(x)\mathrm{d}x}{\int_{\Omega_S}\mathrm{d}x}\ast\int_{\Omega}g(x)\mathrm{d}x$

将 $V(p,\omega)$ 提出来，得到：

$L_o(p,\omega_o)=\frac{\int_{\Omega+}(\boldsymbol{n}\ast\boldsymbol{\omega_i})V(p,\omega_i)\mathrm{d}\omega_i}{\int_{\Omega+}(\boldsymbol{n}\ast\boldsymbol{\omega_i})\mathrm{d}\omega_i}\ast\int_{\Omega+}L_i(p,\omega_i)f_{brdf}(p,\omega_i,\omega_o)\mathrm{d}\omega_i$

立体角 $\mathrm{d}\omega_i$ 可以换成 $\sin{\theta_i}\mathrm{d}\theta\mathrm{d}\varphi$ ，其中 $\cos\theta_i=\boldsymbol{n}\ast\boldsymbol{\omega_i}$ ，上式分母部分替换计算后等于 $\pi$ ，根据最开始做出的三个假设可以得到 $L_i(p,\omega_i)$ 和 $f_{brdf}(p,\omega_i,\omega_o)$ 为常数，最终可以简化原式子到：

$L_o(p,\omega_o)=K\ast L_i\ast\frac{1}{\pi}\ast\int_{\Omega+}\cos{\theta_i}V(p,\omega_i)\mathrm{d}\omega_i$

其中 $K$ 为漫反射系数，相当于brdf函数， $L_i$ 为入射总辐射率， $\frac{1}{\pi}\ast\int_{\Omega+}\cos{\theta_i}V(p,\omega_i)\mathrm{d}\omega_i$ 为AO系数，即环境光遮蔽系数。

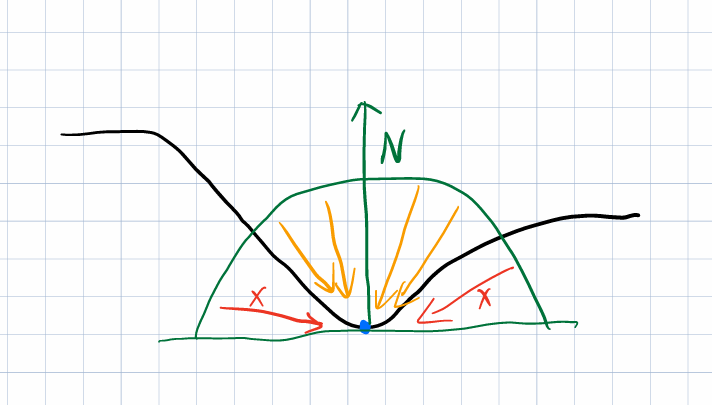
如果此时假设各着色点的 $V(p,\omega_i)$ 为常数1，即可得到最开始的环境光照模型。

计算

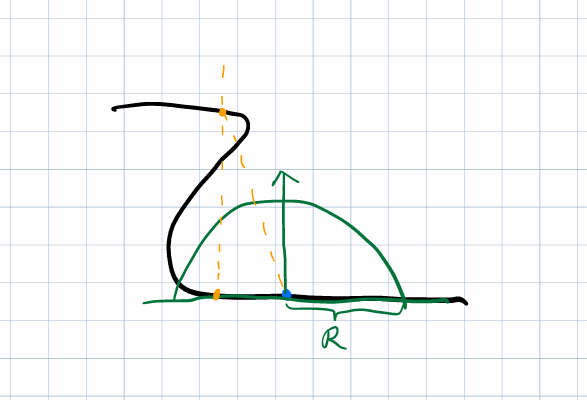
显然需要通过采样计算AO系数，考虑平均采样方法，由于积分变量是立体角，难以对立体角进行采样，将半圆采样视为在半径无限大的半球中采样，在实际工程中，将积分域转换为一个有限半径 $R$ 的半球，那么AO计算的公式为

$AO=\frac{1}{\pi} \sum_{R^2_+}V(p,p_{sample})\cos{\theta_i}$

由于原先无限大的半球被缩小到 $R$ ，距离大于 $R$ 的部分贡献的AO值被忽略，所以AO的计算会比实际情况略小，在实际工程中误差可以接受

同样，由于 $\cos{\theta_i}$ 的计算依赖于法线，在过去的渲染管线中难以获取法线信息，所以在计算时也一并忽略了，AO的计算变为

$AO=\frac{1}{\pi} \sum_{R^2_+}V(p,p_{sample})$

即如图所示

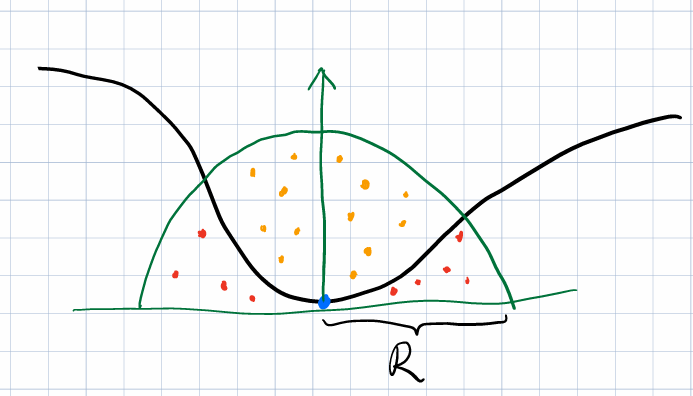
尽管上述理论推导过程中进行了多次近似，但实际使用依然能得到一定的效果。

SSAO

考虑在屏幕空间实现SSAO算法：

屏幕空间的点表示通常为 $(pixelX,pixelY)$ 或者 $(clipX,clipY)$ ，即以像素坐标表示或以纹理坐标表示，为表达其对应的点还需要深度信息，在顶点着色器中改信息可以直接得到，而在像素着色器中需要顶点着色器提供或从深度图中读取。

而后将该点变换到世界空间中，这需要得到VP变换的逆，此时需要得到采样点位置。

判断采样点是否在模型内是一个复杂的计算，应该使用一个更简单的判断方式，考虑顶点的法线空间，该空间内法线指向 $\mathrm{Z}$ 轴正方向，在 $\mathrm{Z}=0$ 平面内创建二维随机向量 $(offsetX,offsetY)$ ，点 $p+(offsetX,offsetY,0)$ 就是采样点，该采样点的 $\mathrm{Z}$ 坐标即深度与着色点相等，将该采样点变换到世界空间中，再变换到屏幕空间中，可以得到点 $p^`$ ，从采样点变换到世界空间需要TBN矩阵，将该点的深度与屏幕空间中深度进行比较，即可得到该采样点是否在物体内。

于是给出以下伪代码

for(auto point : screen)
    pixelPosition = getPixelPosition(); // xyz坐标
    worldPosition = transformToWorldSpace(pixelPosition);
    while(sampleCount--)
    {
        offset = TBN * offset;
        samplePosition = worldPosition + offset; // xyz
        depth = getDepth(samplePosition.xy);
        visibility += (depth > samplePosition.z) ? 1.0 : 0.0;
    }
    visibility = visibility / pi  / sampleCount;

注意到世界空间和观察空间仅做了旋转和平移操作，对于空间关系并没有改变，所以也可以选择在观察空间中进行计算。

缺陷与优化

首先是采样点的问题

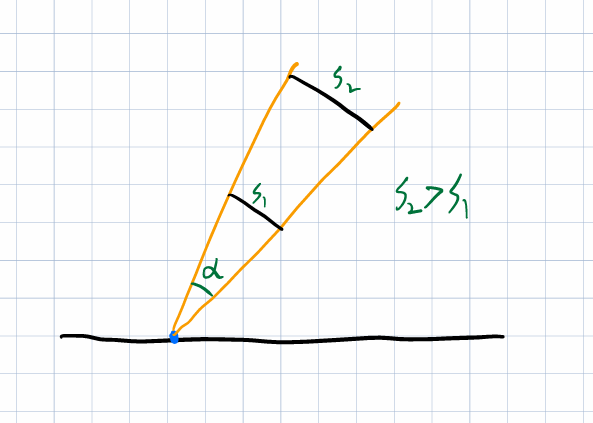
由于原式子计算的是关于立体角的遮挡，当其离散化到采样点计算时，近处采样点的权重显然要比远处的点大，即同样面积的遮挡，更近处遮挡的立体角比更远处要大，显然这个关系遵循平方反比，如果使用均匀采样，将会使计算出的值更小。

可以有两种解决办法，一种是根据采样点离着色点的距离添加权重，二是在更近的地方采样更多的点，第一种方法增加了许多计算量，通常会采用第二种方法。

第二点是边缘错误

当着色点接近边缘的时候，上述算法采样点仅控制法线空间中 $xy$ 的坐标，可以确保不超过采样半径，深度值通过采样获得，组成采样点时距离着色点的位置可能超过半径，导致错误计算，解决方法是加入距离检测，即当采样点距离着色点过远时去掉本次采样结果。